
"…Sesungguhnya Allah itu indah dan menyukai keindahan…," (HR. Muslim)
Arsitek memiliki nilai
tambah apabila ia mampu mengkombinasikan kemampuan teknik dengan
seni. Bagaimanapun, bangunan yang dirancang seharusnya tak hanya kuat, kokoh,
nyaman, dan berfungsi dengan baik; tapi juga indah.
Keindahan, konon, berkolerasi dengan
proporsi. Arsitek dan seniman selama berabad-abad berkutat dengan proporsi
untuk menciptakan komposisi yang indah. namun, sebagai insan yang menyadari bahwa
dirinya adalah makhluk, bukan pencipta, arsitek harus sadar bahwa contoh-contoh
proporsi yang sempurna terdapat dalam ciptaan-Nya.
Adakalanya manusia memang iseng
dan merasa hal tersebut perlu dijelaskan dengan fakta terukur sebelum
ia yakin sepenuhnya. Saya menemukan sebagian penjelasannya dalam buku
"Komposisi Arsitektur" dari Prof. Bob Krier, “Le Modulor” dari Le
Corbusier, dan video "Arsitek-Arsitek
di Alam" dari Harun Yahya.
Krier menjelaskan dengan
Matematika.
Seorang guru di SMP saya dulu, Bu
Elis, pernah berkata: "Elemen paling dasar dari matematika adalah titik. Konon
seorang pemikir matematika berjalan melingkar di padang salju (atau gurun?)
sambil mengetuk-ngetukkan tongkatnya secara berkala dan terbentuklah lingkaran.
Ternyata, lingkaran terdiri dari banyak titik. Begitu pula garis, bidang,
huruf, dan angka."
Tentu saja, titik itu sendiri
bila diperbesar berbentuk lingkaran. Maka kuliah tentang proporsi dari Prof.Krier
dimulai dari pemahaman tentang lingkaran. Persiapkan diri Anda kalau-kalau Anda
merasa bosan. Semoga menjadi pemahaman menarik pada akhirnya.
#1: Lingkaran dibagi 3 sama
besar. Sudut pusat masing-masing bagian sebesar 120˚ seperti terdapat pada
gambar di atas. Artinya ketiga titik sudut kelilingnya dapat membentuk segitiga
sama sisi bersudut 60˚. Bila dibuat sebuah persegi panjang yang memuat segi tiga tersebut, maka didapat persegi panjang dengan perbandingan P : L = 1 : 0.86 = 1.15 : 1.
#2: Lingkaran dibagi 4 sama
besar. Sudut pusat masing-masing bagian 90˚ dan membentuk persegi di dalam
lingkaran. Ambil salah satu segitiga dan satu juringnya, buat satu persegi
panjang yang membungkus keduanya, maka didapat sebuah perbandingan P : L = 1,41
: 1 = 1 : 0,7.
#3: Lingkaran dibagi 5 sama besar. Sudut pusat
tiap juring 72˚ dan membentuk segi lima sama sisi dalam lingkaran. Sudut
Kelilingnya 36˚, karena sudut keliling selalu 1/2 dari sudut pusat. Ambil satu segitiga dari sudut pusat, beserta segitiga dari
sudut kelilingnya, kemudian bungkus dengan persegi panjang dan diperolehlah perbandingan P : L = 1,618 : 1 = 0,618 : 1. Ini adalah perbandingan yang dikenal dengan Golden
Section.
#4: Lingkaran dibagi 10. Mirip
dengan poin #3, namun didapat sebuah persegi panjang di dalam lingkaran dengan
perbandingan P : L = 1,37 : 1. Apabila diambil segmentasi terkecil dari 10
segmen, maka diperoleh persegi panjang dengan P : L = 3,73 : 1.
#5: Lingkaran dibagi 6 sama
besar. Sudut-sudut pusat setiap juringnya adalah 60˚. Di dalam lingkaran dapat
dibentuk sebuah persegi panjang dengan perbandingan P : L = 1,732 : 1.
#6: Lingkaran dibagi 7 bagian.
Sudut-sudut pusatnya 51,4˚. Perbandingan P : L dari persegi panjang yang
terbentuk adalah 2,07 : 1.
Hasil pembagian lingkaran menjadi
3, 4, 5, 6, 8, dan 10 bagian menghasilkan varian persegi panjang dengan
proporsi bebeda-beda. Berikut rangkumannya bila semua persegi panjang tersebut
disuperimposisikan:
Dapat dilihat bahwa proporsi yang
terbentuk dari hasil pembagian lingkaran tak hanya terbatas pada golden
section. Prof. Krier memberikan beberapa contoh menarik untuk perbandingan
proporsi tersebut di alam.
1. Aalisis Proporsi Kuda. Berdasarkan analisis Prof. Krier ternyata kuda memiliki proporsi golden section. Bisa diperhatikan pada gambar berikut.
2. Analisis Proporsi Struktur 5
Daun. Ternyata proporsi daun ini sesuai dengan pembagian lingkaran
menjadi 5 bagian. Yang menarik adalah percabangannya yang bukan berada di pusat
lingkaran, melainkan di salah satu persilangan dari bentuk bintang.
3. Analisis Proporsi Daun Beech,
Walnut, Oak. Ternyata ketiga daun ini memiliki proporsi yang sama dengan hasil pembagian
lingkaran menjadi 3 dan 6 bagian. Proporsinya adalah 1 : 1,15 ; 1 : 1,7 ; dan 1
: 3.
Le Modulor
Le Corbusier (1887-1965), arsitek dan pemikir
ternama dari Swiss, menjelaskan adanya proporsi yang sempurna dalam salah satu
ciptaan-Nya yang sangat kita kenal: manusia.
Le Corbusier melakukan pengukuran pada tubuh manusia dan menemukan fakta yang menarik. Pusar, misalnya, rupanya membagi tubuh
manusia dalam proporsi Golden Section. Jarak dari puncak kepala ke pusar dibagi
dengan garis leher juga merupakan pembagian Golden Section. Begitu pula dengan
ketiak. Proporsi telinga pun merupakan rangkaian Golden Section. terdapat keyentuan ukuran yang menarik lainnya. Misalnya kelipatan 7. Tinggi badan manusia
umumnya tujuh kali panjang telapak kakinya. Begitu pun pada
beberapa bagian tubuh lainnya. Bukankah memang manusia diciptakan dengan sebaik-baik rupa?
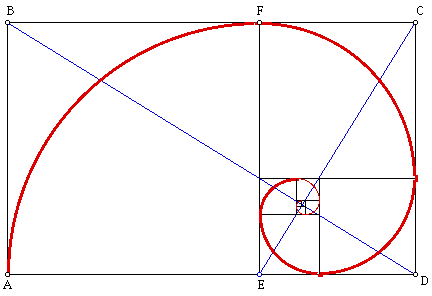
Apa itu Golden Section? Contoh
sederhana dari Golden Section adalah bidang persegi panjang dengan proporsi 1 : 1,618. Mengapa ia disebut
Golden, dapat dijelaskan dengan gambar berikut.
Persegi panjang dengan proporsi demikian, apabila dikurangi oleh persegi seukuran lebarnya, akan menyisakan persegi panjang kecil yang juga golden section. Demikian seterusnya. Apabila lebar perseginya ditarik menjadi jari-jari lingkaran, maka busur lingkaran tersebut akan menerus membentuk spiral yang sempurna. Konon proporsi Golden Section
telah digunakan oleh manusia jauh dalam peradaban-peradaban kuno. Contoh di
alam benda-benda yang berproporsi Golden Section adalah keong laut, kuda
(seperti dijelaskan Krier), dan manusia (seperti yang diteliti oleh Le
Corbusier).












yayay,,,,
ReplyDeletemantrap...
my home,,
http://udinelmanaf.blogspot.com/